Der t-Test für unabhängige Stichproben als GLM und PGM

The proof of the pudding is in the eating. Von daher möchte ich an einem kleinen Beispiel zeigen, wie Generalisierte Lineare Modelle (GLMs), Probabilistische Graphische Modelle (PGMs) und Bayesianische Methoden praktisch zusammenspielen können. Was bietet sich besseres an, als der t-Test für unabhängige Stichproben? Um eine gewisse Vergleichbarkeit zu gewährleisten, beziehe ich mich auf das Beispiel zum t-Test in Bortz, Statistik, 6. Auflage (Tabelle 5.1., Seite 142). Zur praktischen Demonstration verwende ich die Software R und OpenBUGS. Die verwendeten Dateien finden sich hier.

Der t-Test für unabhängige Stichproben als GLM

Den meisten dürfte bekannt sein, dass die Fragestellung hinter dem t-Test sich auch mit der multiplen Regression, bzw. dem Allgemeinen Linearen Modell (ALM) bearbeiten lässt. Im Beispieldatensatz aus dem Bortz geht es darum zu prüfen, ob sich Männer und Frauen hinsichlich ihrer Belastbarkeit unterscheiden. Mit R geht das ganz einfach mit der Funktion glm().

# t-test_ua.R
 
# Laden der Daten
data<-read.table("B_5_1.csv", sep=",", head=T)
 
# Anpassung eines GLM mit Identitäts-Link-Funktion
m1<-glm(belast~geschl, data=data, family="gaussian")
summary(m1)

Es wird ein GLM mit Identitäts-Link-Funktion an die Daten angepasst. R liefert folgenden Output:

Call:
glm(formula = belast ~ geschl, family = "gaussian", data = data)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-18.242   -9.732   -2.221    9.289   25.800  

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  103.200      2.130  48.452   <2e-16 ***
geschlw        1.042      3.057   0.341    0.734    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 

(Dispersion parameter for gaussian family taken to be 158.7827)

    Null deviance: 10498  on 67  degrees of freedom
Residual deviance: 10480  on 66  degrees of freedom
AIC: 541.54

Number of Fisher Scoring iterations: 2

Der mit Intercept bezeichnete Schätzer ist der vorhergesagte Mittelwert der Belastbarkeit der Männer und der Schätzer geschlw ist der Kontrast der Frauen zu dieser Baseline. Das bedeutet, dass Frauen einen um 1.042 Punkte höheren vorhergesagten Wert auf der Belastbarkeits-Skala aufweisen. Allerdings ist anhand des t-Werts von 0.341 deutlich ersichtlich, dass dieser Unterschied statistisch nicht signifikant ist. Dieses Ergebnis deckt sich im Wesentlichen mit dem Ergebnis im Bortz, wo ein t-Wert von -0.33 verzeichnet ist.

Der t-Test für unabhängige Stichproben als PGM

Das eben verwendete GLM lässt sich auch als grafisches Modell darstellen. Abbildung 1 zeigt die grafische Repräsentation.

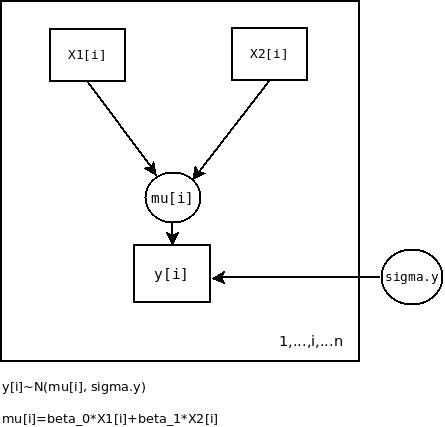
Abbildung 1: Das GLM für den t-Test für unabhängige Stichproben als PGM

y[i] bezeichnet die Werte der abhängigen Variable und x1[i] und x2[i] bezeichnen die Werte der jeweiligen Prädiktoren in der Design-Matrix. mu[i] ist der lineare Prädiktor des Modells, der nach Maßgabe des zugrundeliegenden Designs linear zerlegt wird. sigma.y ist die Streuung der Residuen in der Population. Die Pfeile bezeichnen Abängigkeiten zwischen den Knoten des Netzwerks. Der Rahmen (plate notation) um die Knoten symbolisiert, dass $n$ Beobachtungen vorliegen. Formal lässt sich das Modell relativ einfach darstellen:

$y_i \sim N(\mu_i, \sigma_y^2) \mu_i=\beta_0 x_{1i} + \beta_1 x_{2i}$

Es wird also angenommen, dass die beobachteten Werte $y_i$ einer Normalverteilung mit der Mittelwertsstruktur $\mu_i$ und der Varianz $\sigma_y^2$ entstammen. Oder anders gesagt, es wird angenommen, dass die Residuen in der Population mit der Varianz $\sigma_y^2$ normal verteilt sind. Wenn die Dummy-Codierung für $x_{1i}$ der Spezifikation einer Konstanten entspricht, handelt es sich also um nichts anderes, als um eine einfache lineare Regression in grafischer Darstellung.

Bayesianische Bestimmung der Parameter

Die Parameter $\beta_0$ , $\beta_1$ und die Varianz $\sigma_y^2$ müssen aus den Daten geschätzt werden. Wie dies auf Bayesianische Art mit Hilfe der MCMC-Methode, R und OpenBUGS geschehen kann, sei kurz gezeigt. Zunächst muss eine Datei mit der Modellspezifikation für OpenBUGS erstellt und gespeichert werden.

# t-test_ua.txt
model
{
  # Likelihood
  for (i in 1:n)
  {
  y[i] ~ dnorm (mu[i], tau.y)
  mu[i]<-beta0*X[i,1]+beta1*X[i,2]
  }
  # Prior-Distributions
  beta0 ~ dnorm(0, 1.0E-6)
  beta1 ~ dnorm(0, 1.0E-6)
  tau.y <- pow(sigma.y, -2)
  sigma.y ~ dunif (0, 1000)
  # Cohen's delta
  delta<-(beta1)/sigma.y
}

Die Spezifikation des Modells erfolgt im Abschnitt #Likelihood. Anschließend werden die Prior-Verteilungen spezifiziert, die hier relativ uninformativ gehalten sind. Als besonderer Bonus wird die Posterior-Verteilung von Cohen's delta auf Basis des MCMC-Prozesses erzeugt.

OpenBUGS wird durch das R-Skript angesteuert, das auch die Daten an OpenBUGS übergibt.

 
library(R2OpenBUGS)
# Vorbereitung der Daten zur 
# Übergabe an OpenBUGS
y<-data$belast
X<-model.matrix(m1)
n<-length(y)
data<-list("y","X", "n")
 
# Spezifikation der zu bestimmenden Parameter
parameters<-c("beta0", "beta1", "sigma.y", "delta")
 
# Übergabe an OpenBUGS
output<-bugs(data, inits=NULL, parameters, model.file="t-test_ua.txt",
    n.chains=2, n.iter=5000, n.burnin=1000)
 
# Ausgabe der Ergebnisse
print(output, digits=2)
 
# Histogramm von beta1
hist(beta1,100)
# Histogramm von Cohen's delta
hist(delta,100)

Um die Konvergenz des Markov-Prozesses zu überprüfen, kommen zwei Markov-Ketten zum Einsatz. Der Prozess durchläuft 5000 Iterationen, wobei die Burn-In-Phase 1000 Iterationen beträgt. Die Startwerte des Markov-Prozesses werden im Beispiel zufällig erzeugt.

OpenBUGS liefert folgenden Output:

Inference for Bugs model at "t-test_ua.txt", 
Current: 2 chains, each with 5000 iterations (first 1000 discarded)
Cumulative: n.sims = 8000 iterations saved
              mean   sd   2.5%    25%    50%    75%  97.5% Rhat n.eff
beta0       103.25 2.14  99.06 101.80 103.20 104.70 107.40    1  8000
beta1         0.99 3.07  -5.06  -1.02   0.97   2.98   7.06    1  8000
sigma.y      12.84 1.15  10.82  12.03  12.75  13.55  15.35    1  8000
delta         0.08 0.24  -0.39  -0.08   0.08   0.23   0.55    1  8000
deviance    538.62 2.55 535.80 536.80 538.00 539.70 545.00    1  4300

For each parameter, n.eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor (at convergence, Rhat=1).

DIC info (using the rule, pD = Dbar-Dhat)
pD = 2.9 and DIC = 541.5
DIC is an estimate of expected predictive error (lower deviance is better).

Von Interesse sind hier besonders die Mittelwerte und Perzentile der Posterior-Verteilungen und Rhat. Der Schätzer für die mittlere Belastbarkeit der Männer beträgt 103.25 und der geschätzte Kontrast der Frauen zum Mittelwert der Männer beträgt 0.99. Das 95%-Kredibilitäts-Intervall für $\beta_1$ liegt zwischen -5.06 und 7.06. Damit ist der Unterschied zwischen Männern und Frauen statistisch nicht signifikant. Der Schätzer für Cohen's delta beträgt 0.08. Dieses Ergebnis ist mit dem Resultat im Bortz kongruent. Zudem wurde das 95%-Kredibilitäts-Intervall für Cohen's delta ermittelt. Dieses Intervall liegt zwischen -0.39 und 0.55, was ebenfalls darauf hindeutet, dass der Unterschied zwischen Männern und Frauen hinsichtlich der Belastbarkeit statistisch nicht signifikant ist. Die Statistik Rhat zeigt an, dass die zwei eingesetzten Markov-Ketten gegen die Posterior-Verteilung der Parameter konvergieren.

Was auffällt ist, dass in der Ausgabe keine p-Werte vorkommen. Das ist nicht weiter tragisch, da die Inferenz auf Basis der Kredibilitäts-Intervalle geschieht. Wer aber dennoch nicht auf p-Werte verzichten möchte, kann diese einfach aus den Posterior-Verteilungen berechnen. Zum Abschluss sei hier noch das Histogramm der Posterior-Verteilung von Cohen's delta dargestellt.

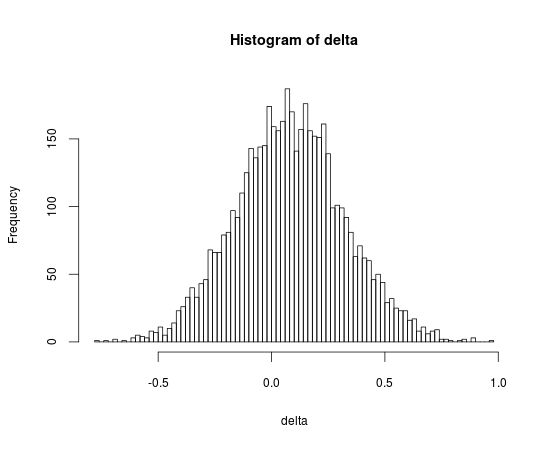
Abbildung 2: Posterior-Verteilung von Cohen's delta

Das war zugegebener Maßen ziemlich viel Information auf einmal und Anspruch dieser Blog-Post kann es nicht sein, die Hintergründe der hier verwendeten Verfahren umfassend zu erklären. Den interessierten Leser oder die interessierte Leserin verweise ich auf die Literatur. Mir war es jedoch wichtig, einmal an einem einfachen Beispiel zu zeigen, wie GLMs, PGMs und Bayesianische Methoden ineinandergreifen können.

Als Übung empfehle ich zu überlegen, wie das grafische Modell und der OpenBUGS-Code im Falle der multiplen Regression aussehen müssten. Bonuspunkte gibt es für die Erzeugung der Posterior-Verteilung für den Determinations-Koeffizienten, bzw. $\eta^2$ . Interessant wäre auch ein systematischer Vergleich der hier dargestellten Methode zur Erzeugung von Kredibilitäts-Intervallen für Effektstärke-Indices mit der „frequentistischen" Methode zur Erzeugung von Konfidenz-Intervallen auf Basis von nichtzentralen Verteilungen.

Georg Hosoya

personal blog

Der t-Test für unabhängige Stichproben als GLM und PGM